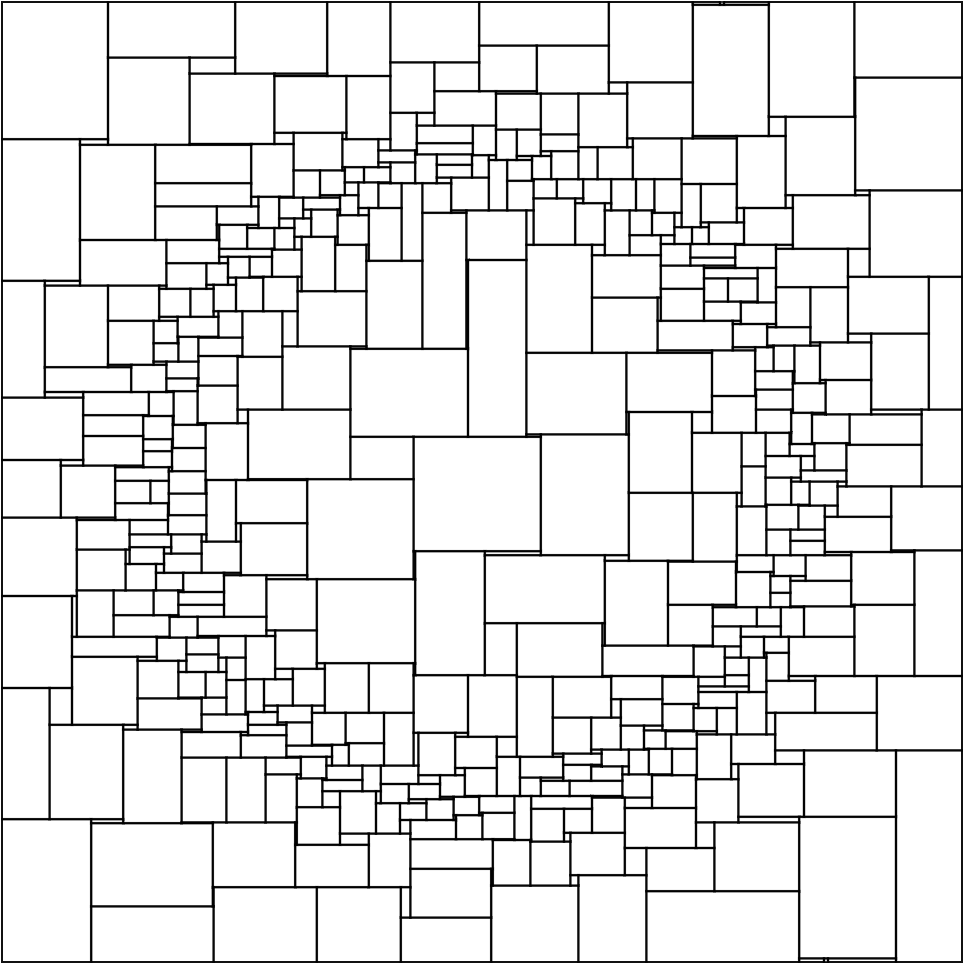
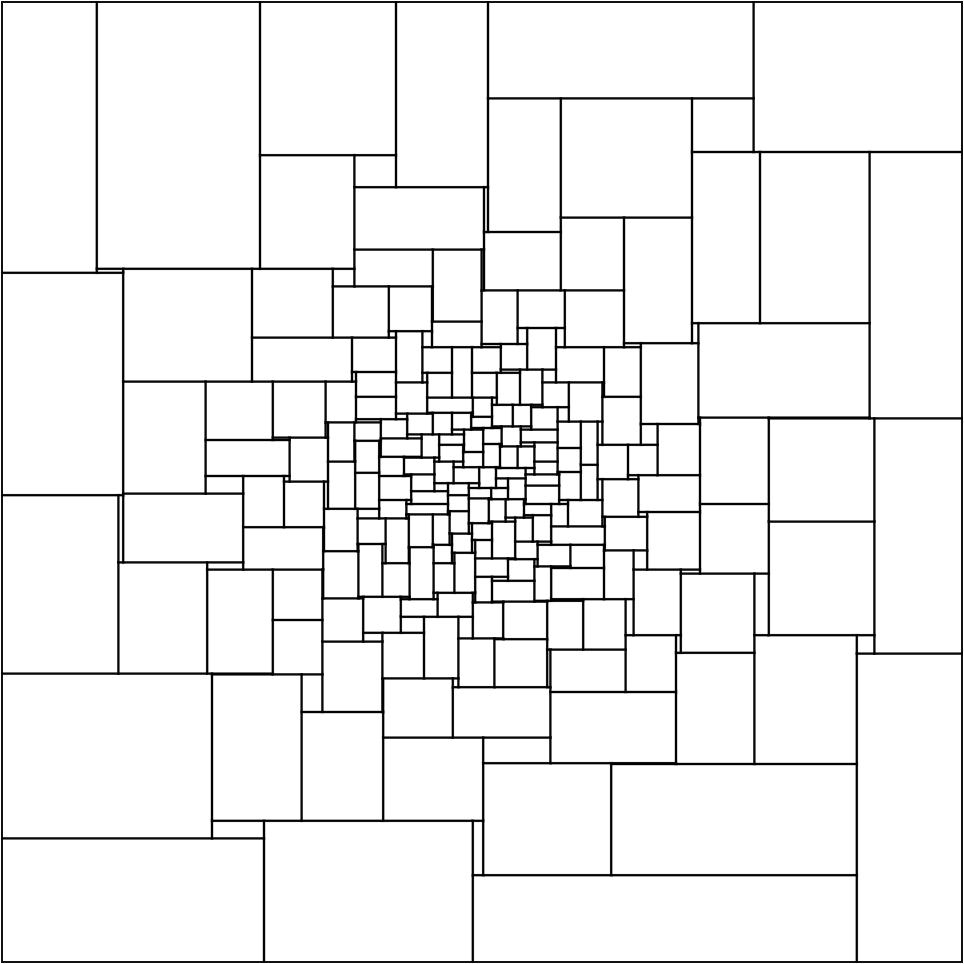
Rectangle Tiling

Tiling of an area with rectangles - here taking a set of poisson-disc distributed points. Shrinking the generated rectangles a bit (right) shows the tiling maybe in a better way:

Playing with the set of starting points can lead to more interesting patterns:

As I did not know or find a good algorithm to divide an area into rectangles, I am using this method:

1. use a set of starting points to grow rectangles around them until the get blocked by other rectangles
2. find a point that is still not covered and grow another rectangle around it until it is blocked
3. repeat 2. until the full area is covered

This video shows how that is working with the starting points marked as red dots:

This algorithm is not really fast, especially given a larger number of starting points, but is optimized a bit further by starting with larger steps of growth then iteratively refine the steps when the rectangle is starting to get blocked.
To avoid problems with floating point edge cases, this is done in pixel, i.e., in integer space.